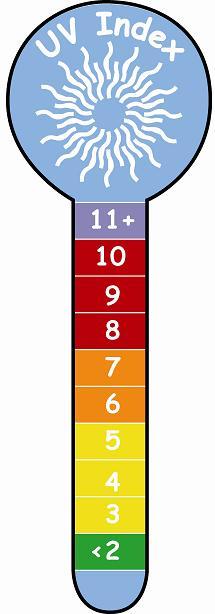
Calculating the UV Index
The U.S. National Weather Service calculates the UV Index using a computer model that relates the ground-level strength of solar ultraviolet (UV) radiation to forecasted stratospheric ozone concentration, forecasted cloud amounts, and elevation of the ground.
The calculation done by some other nations also includes ground observations. The calculation starts with measurements of current total ozone amounts over the entire globe, obtained via two satellites operated by the National Oceanic and Atmospheric Administration. These data are used to produce a forecast of stratospheric ozone levels for the next day at many points across the country. A computer model uses the ozone forecast and the incident angle of sunlight at each point to calculate the strength of UV radiation at ground level. Sunlight angle is determined by latitude, day of year, and time of day (solar noon). The strength of UV radiation is calculated for several wavelengths between 280 and 400 nm, the full spectrum of UVB (280-314 nm) and UVA (315-400 nm) radiation.
Ozone in the atmosphere absorbs (attenuates) shorter UV wavelengths more strongly than longer wavelengths. The strength of ground-level UV radiation differs significantly across the UV spectrum. As an example, UV strengths for a point might be calculated as shown in the table below. (These are hypothetical values. A National Weather Service chart shows typical UV irradiance values.)
| Wavelength | Strength |
|---|---|
| 290nm | 4 |
| 320nm | 26 |
| 400nm | 30 |
The next step in the calculation adjusts for the sensitivity of human skin to UV radiation. Shorter UV wavelengths cause more skin damage than longer UV wavelengths of the same intensity. To account for this response, calculated UV strength is weighted (adjusted) at each wavelength using a function called the McKinlay-Diffey erythema action spectrum.
Continuing with our example, the table below gives skin response weighting factors for the UV wavelengths. (These are hypothetical values for the example, not actual McKinlay-Diffey weighting factors.) We multiply the ground-level UV strength by the weighting factor to calculate the result, the effective strength of the UV radiation, at each wavelength.
| Wavelength | Strength | Weight | Result |
|---|---|---|---|
| 290nm | 4 | 15 | 60 |
| 320nm | 26 | 5 | 130 |
| 400nm | 30 | 3 | 90 |
Next, the effective UV strength at each wavelength across the 290 to 400 nm spectrum is summed (integrated), giving a value that represents the total effect of UV radiation on skin. In our example, the total UV effect is 280 (60 + 130 + 90).
The next step of the calculation adjusts for the effects of elevation and clouds. UV intensity increases about 6% per kilometer elevation above sea level. Clouds absorb UV radiation, reducing ground-level UV intensity. Clear skies allow virtually 100% of UV to pass through, scattered clouds transmit 89%, broken clouds transmit 73%, and overcast skies transmit 31%.
For our example, let us assume that the elevation is 1 kilometer and there are broken clouds overhead. The total UV effect, adjusted 6% for elevation and 73% for clouds, would be calculated as:
280 x 1.06 x 0.73 = 216.7
The final step of the calculation scales the total UV effect, dividing it by 25 and rounding to the nearest whole number. The result is a number that usually ranges from 0 (darkness or very weak sunlight) to the mid-teens (very strong sunlight). This value is the UV Index.
For our example, the UV Index would be:
216.7 / 25 = 8.7, rounded to 9
